In abstract terms, a helical undulator consist of a cylindrical "gap" region surrounded by a cylindrical
"excitation" region. Within the gap, a rotating dipole field with longitudinal and azimuthal period
and wavenumber
exists. The excitation region consists of helically distributed material exhibiting a permanent dipole moment
and possibly permeable material of variable moment
resulting in a field
. In a current free region, Maxwell's equations are satisfied by a divergence free,
,
irrotational,
,
field, and a scaler magnetic potential
exists, satisfying Poisson's equation
.
is 0 on axis, at
,
and is continuous across boundaries.
By representing the distribution of
,
and consequently,
as Fourier series, a boundary value problem solution of an inhomogeneous, modified Bessel differential equation
describes the generated fields. In the very simple case of a double helix of ideal magnet material with a
continuously rotating vector
,
the gap fields are:
,
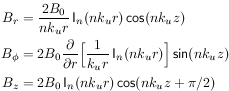where .
is the magnets' residual field.
is gap radius,
is outer magnet radius, and
is harmonic number.
and
are the modified Bessel functions. The added complication of introducing non-linear permeable material necessitates
a numerical solution, and code for that purpose is under development. The basic form of the fields in the gap is
expected to change little, however, just the absolute field strength and harmonic content.
and wavenumber
exists. The excitation region consists of helically distributed material exhibiting a permanent dipole moment
and possibly permeable material of variable moment
resulting in a field
. In a current free region, Maxwell's equations are satisfied by a divergence free,
,
irrotational,
,
field, and a scaler magnetic potential
exists, satisfying Poisson's equation
.
is 0 on axis, at
,
and is continuous across boundaries.
By representing the distribution of
,
.
is the magnets' residual field.
is gap radius,
is outer magnet radius, and
is harmonic number.
and
are the modified Bessel functions. The added complication of introducing non-linear permeable material necessitates
a numerical solution, and code for that purpose is under development. The basic form of the fields in the gap is
expected to change little, however, just the absolute field strength and harmonic content.
